
[ITEM]

 [/ITEM]
[/ITEM]


Matlab Program For Dolph Chebyshev Array Definition 5,7/10 6099 votes
Volkswagen Sharan Volkswagen Sharan is a 7-seat MPV from German automaker Volkswagen and was introduced in 1995. Foljksvagen sharan rukovodstvo po ekspluatacii skachatj besplatno. The name?Sharan?
Frank gambale technique book 1 pdf download. Players will learn to extend their sense of harmony by the superimposition of chord forms which are familiar, as well as a world of new ones.
Side-Lobe Level in (4.45) Thus, gives side-lobes which are below the main-lobe peak. Since the side lobes of the Dolph-Chebyshev window transform are equal height, they are often called ``ripple in the stop-band' (thinking now of the window transform as a lowpass ). The smaller the ripple specification, the larger has to become to satisfy it, for a given window length. The Chebyshev window can be regarded as the of an optimal Chebyshev having a zero-width pass-band ( i.e., the main lobe consists of two ``'--see Chapter regarding more generally). In, the function chebwin(M,ripple) computes a length Dolph- having a level ripple below that of the peak.
For example, w = chebwin(31,60); designs a length window with side lobes at (when the main-lobe peak is normalized to 0 ). Figure shows the Dolph- and its transform as designed by chebwin(31,40) in, and Fig. Shows the same thing for chebwin(31,200). As can be seen from these examples, higher levels are associated with a narrower and more discontinuous endpoints.

Figure: The length Dolph-Chebyshev window with ripple (side-lobe level) specified to be. Figure shows the Dolph-Chebyshev window and its transform as designed by chebwin(101,40) in Matlab. Note how the endpoints have actually become impulsive for the longer window length.
W = chebwin(L,r) returns the column vector w containing the length L Chebyshev window whose Fourier transform sidelobe magnitude is r dB below the mainlobe magnitude. The default value for r is 100.0 dB. This MATLAB function returns the values of the Dolph-Chebyshev window object H as a double-precision column vector.
The, in contrast, is constrained to be monotonic away from its center in the time domain. The ``equal ripple' property in the perfectly satisfies worst-case side-lobe specifications. However, it has the potentially unfortunate consequence of introducing ``' at the window endpoints. Such impulses can be the source of ``pre-echo' or ``post-echo' which are time-domain effects not reflected in a simple side-lobe level specification. This is a good lesson in the importance of choosing the right error criterion to minimize.
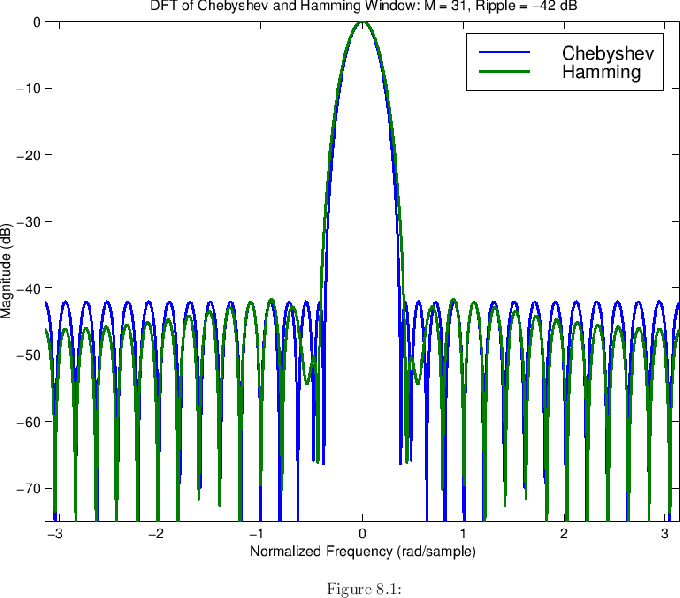
In this case, to avoid impulse endpoints, we might add a continuity or monotonicity constraint in the time domain (see § for examples). Chebyshev and Compared Figure shows an overlay of Hamming and Dolph- transforms, the ripple parameter for chebwin set to to make it comparable to the Hamming level. We see that the monotonicity constraint inherent in the Hamming window family only costs a few of deviation from optimality in the Chebyshev sense at high frequency. Dolph- Theory In this section, the main elements of the theory behind the Dolph-Chebyshev window are summarized. Chebyshev Polynomials.
Interference Removal Using Sidelobe Canceller A common requirement when synthesizing beam patterns is pointing a null towards a given arrival direction. This helps suppress interference from that direction and improves the signal-to-interference ratio. The interference is not always malicious- an airport radar system may need to suppress interference from a nearby radio station.
In this case, the position of the radio station is known and a sidelobe cancellation algorithm can be used to remove the interference. Sidelobe cancellation is useful for suppressing interference that enters through the array's sidelobes. In this case, because the interference direction is known, the algorithm is simple.
Form a beam that points towards the interference direction, then scale the beam weights and subtract scaled weights from the weights for the beam patterns that point towards any other look direction. This process always places a strong null in the interference direction. The following example shows how to design the weights of the radar so that it scans between -30 and 30 degrees yet always keeps a null at 40 degrees. Assume that the radar uses a 10-element ULA that is parallel to the ground and that the known radio interference arrives from 40 degrees azimuth.
- Author: admin
- Category: Category

Matlab Program For Dolph Chebyshev Array Definition 5,7/10 6099 votes
Volkswagen Sharan Volkswagen Sharan is a 7-seat MPV from German automaker Volkswagen and was introduced in 1995. Foljksvagen sharan rukovodstvo po ekspluatacii skachatj besplatno. The name?Sharan?
Frank gambale technique book 1 pdf download. Players will learn to extend their sense of harmony by the superimposition of chord forms which are familiar, as well as a world of new ones.
Side-Lobe Level in (4.45) Thus, gives side-lobes which are below the main-lobe peak. Since the side lobes of the Dolph-Chebyshev window transform are equal height, they are often called ``ripple in the stop-band' (thinking now of the window transform as a lowpass ). The smaller the ripple specification, the larger has to become to satisfy it, for a given window length. The Chebyshev window can be regarded as the of an optimal Chebyshev having a zero-width pass-band ( i.e., the main lobe consists of two ``'--see Chapter regarding more generally). In, the function chebwin(M,ripple) computes a length Dolph- having a level ripple below that of the peak.
For example, w = chebwin(31,60); designs a length window with side lobes at (when the main-lobe peak is normalized to 0 ). Figure shows the Dolph- and its transform as designed by chebwin(31,40) in, and Fig. Shows the same thing for chebwin(31,200). As can be seen from these examples, higher levels are associated with a narrower and more discontinuous endpoints.

Figure: The length Dolph-Chebyshev window with ripple (side-lobe level) specified to be. Figure shows the Dolph-Chebyshev window and its transform as designed by chebwin(101,40) in Matlab. Note how the endpoints have actually become impulsive for the longer window length.
W = chebwin(L,r) returns the column vector w containing the length L Chebyshev window whose Fourier transform sidelobe magnitude is r dB below the mainlobe magnitude. The default value for r is 100.0 dB. This MATLAB function returns the values of the Dolph-Chebyshev window object H as a double-precision column vector.
The, in contrast, is constrained to be monotonic away from its center in the time domain. The ``equal ripple' property in the perfectly satisfies worst-case side-lobe specifications. However, it has the potentially unfortunate consequence of introducing ``' at the window endpoints. Such impulses can be the source of ``pre-echo' or ``post-echo' which are time-domain effects not reflected in a simple side-lobe level specification. This is a good lesson in the importance of choosing the right error criterion to minimize.
In this case, to avoid impulse endpoints, we might add a continuity or monotonicity constraint in the time domain (see § for examples). Chebyshev and Compared Figure shows an overlay of Hamming and Dolph- transforms, the ripple parameter for chebwin set to to make it comparable to the Hamming level. We see that the monotonicity constraint inherent in the Hamming window family only costs a few of deviation from optimality in the Chebyshev sense at high frequency. Dolph- Theory In this section, the main elements of the theory behind the Dolph-Chebyshev window are summarized. Chebyshev Polynomials.
Interference Removal Using Sidelobe Canceller A common requirement when synthesizing beam patterns is pointing a null towards a given arrival direction. This helps suppress interference from that direction and improves the signal-to-interference ratio. The interference is not always malicious- an airport radar system may need to suppress interference from a nearby radio station.
In this case, the position of the radio station is known and a sidelobe cancellation algorithm can be used to remove the interference. Sidelobe cancellation is useful for suppressing interference that enters through the array's sidelobes. In this case, because the interference direction is known, the algorithm is simple.
Form a beam that points towards the interference direction, then scale the beam weights and subtract scaled weights from the weights for the beam patterns that point towards any other look direction. This process always places a strong null in the interference direction. The following example shows how to design the weights of the radar so that it scans between -30 and 30 degrees yet always keeps a null at 40 degrees. Assume that the radar uses a 10-element ULA that is parallel to the ground and that the known radio interference arrives from 40 degrees azimuth.